在数学的广阔天地里，排列与组合是两个既基础又迷人的领域，它们不仅在数学理论中占据重要地位，还广泛应用于计算机科学、统计学、物理学等多个学科，我们将聚焦于排列中的一个有趣概念——逆序数，并揭开排列“35142”的逆序数之谜。

逆序数定义初探

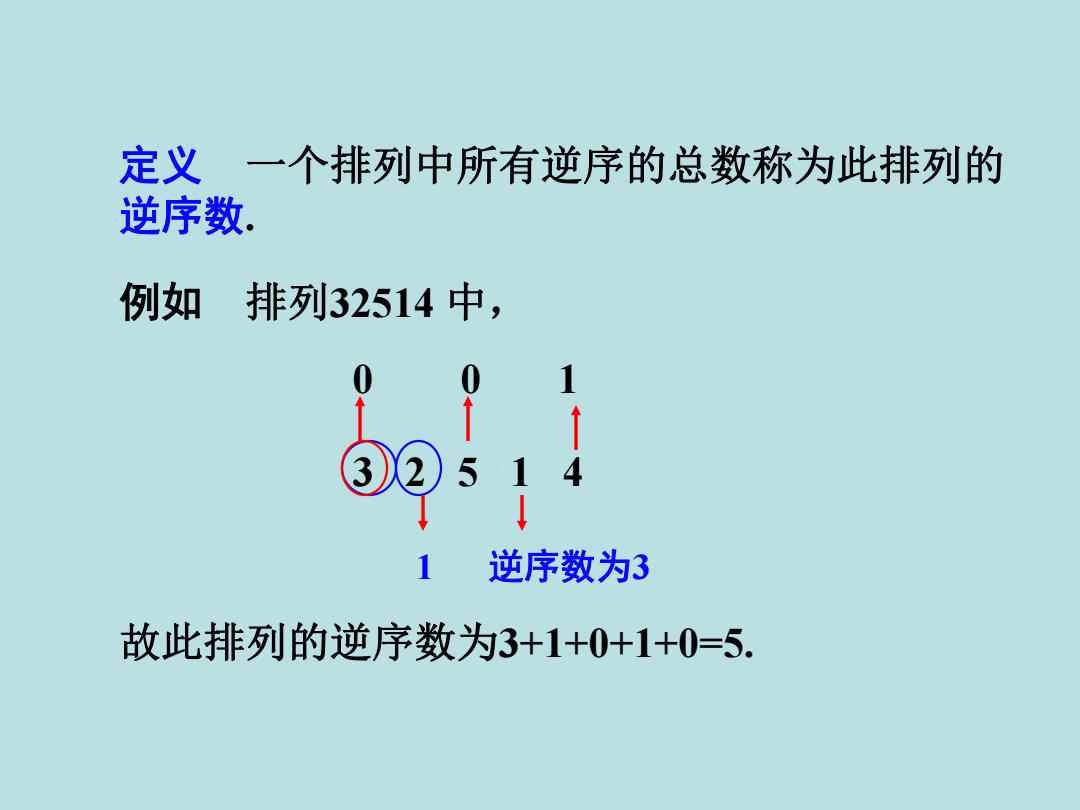
逆序数，也称为逆序对的数量，是衡量一个排列中元素间相对顺序不和谐程度的量度，对于一个由n个不同元素组成的排列P，如果P中的第i个元素位于第j个元素之后（i<j且P[i] > P[j]），则称(i, j)为P的一个逆序对，在排列“35142”中，数字“3”和“5”的相对位置就构成了一个逆序对。

排列35142的逆序数计算

我们来具体计算排列“35142”的逆序数，我们列出这个排列的所有元素：3、5、1、4、2，我们逐一检查每对元素,判断是否存在逆序关系：

• 3与5：不构成逆序对（因为3<5且3在5之前）
• 3与1：构成一个逆序对（因为3>1且3在1之后）
• 3与4：构成一个逆序对（因为3>4且3在4之后）
• 3与2：构成一个逆序对（因为3>2且3在2之后）
• 5与1、4、2：均不构成逆序对（因为5是排列中最大的数,它之前的所有数都小于它）
• 1与4：不构成逆序对（因为1<4且1在4之前）
• 1与2：不构成逆序对（同理）
• 4与2：不构成逆序对（因为4>2但它们相邻且不形成“>”关系）

排列“35142”中共有3个逆序对，即(3,1)、(3,4)和(3,2),该排列的逆序数为3。

逆序数的性质与意义

逆序数的概念虽然简单，但其背后蕴含着丰富的数学性质和实际应用价值，它反映了排列中元素间相对顺序的“混乱程度”，一个完全有序的排列（如1,2,3,...,n）的逆序数为0，而完全无序的排列（如n,n-1,...,2,1）的逆序数为n(n-1)/2，对于一般的排列而言，其逆序数的大小直接反映了该排列的“无序化”程度。

逆序数在算法设计和数据分析中也有着重要应用，在计算机科学中，快速排序算法的效率就与待排序序列的初始逆序数密切相关，一个初始逆序数高的序列可能需要更多的比较和交换操作才能完成排序,从而影响算法的总体性能。

在统计学中，逆序数可以用来衡量数据集的随机性或偏态程度，一个随机排列的逆序数通常接近其可能的最小值或最大值的一半,这为数据分析提供了额外的视角和工具。

数学之美：从逆序数到更广阔的数学世界

通过对排列“35142”的逆序数的计算，我们不仅解决了一个具体问题，还窥见了数学之美及其在更广泛领域中的应用潜力，从简单的计数问题到复杂的算法设计，从理论探讨到实际应用,数学以其独特的魅力和严谨的逻辑连接着世界的每一个角落。

更进一步地，逆序数的概念可以延伸到更高级的数学领域，如组合数学中的错排问题、概率论中的随机游走模型等，在这些领域中，逆序数不仅是理解问题本质的关键,也是推动科学进步的重要工具。

排列“35142”的逆序数为3，这一简单的结论背后蕴含着丰富的数学思想和广泛的应用价值，它不仅是我们理解排列和组合理论的一个窗口，也是连接基础数学与高级应用的一座桥梁，通过探索这样的数学问题，我们不仅能够加深对数学原理的理解，还能激发对未知领域的好奇心和探索欲，在数学的海洋里航行，每一次发现都是对智慧的一次洗礼，每一次思考都是对自我边界的一次拓展，让我们继续在这条充满挑战与惊喜的路上前行,探索数学的无限魅力。