在数学的广阔天地中，排列与组合作为离散数学的重要分支，不仅在理论研究中占据一席之地，也在实际应用中发挥着不可小觑的作用，当我们探讨排列的逆序数时，一个具体的例子——排列35412的逆序数，便成为了一个既具代表性又充满挑战的数学小课题，本文将从基础概念出发，逐步深入,带领读者一探排列35412的逆序数之谜。

逆序数定义与基础概念

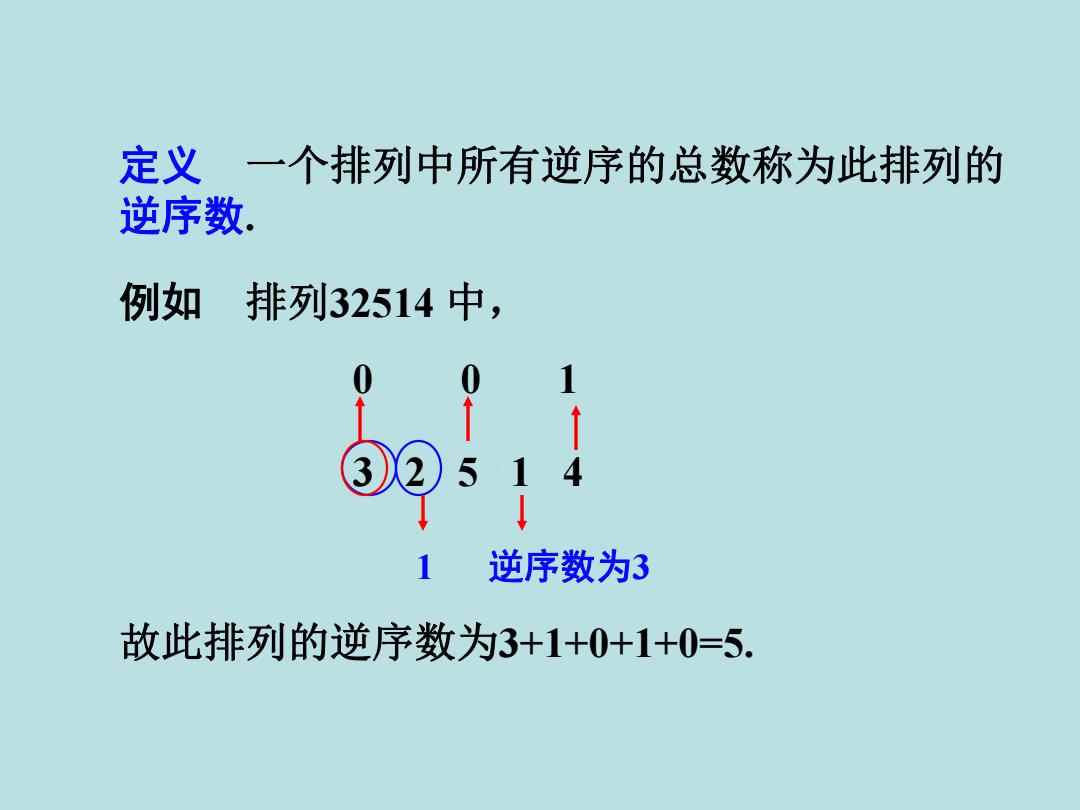
在探讨排列35412的逆序数之前，我们先来明确几个关键概念，逆序数，也称为逆序对数或倒序数，是衡量一个排列中元素顺序颠倒程度的量度，对于一个由n个不同元素构成的排列P，如果P中的第i个元素位于第j个元素之前（i > j且P[i] > P[j]），则称(i, j)为一个逆序对,一个排列的逆序数即为其中所有逆序对的数量之和。

排列35412的直观理解

排列35412由五个数字组成，其本身是一个自然数的递增序列被打乱后的结果，直观上，我们可以发现这个排列并不包含任何逆序对（即不存在i > j且P[i] > P[j]的情况），因为每个数字都位于其“自然位置”之前或之后没有更大的数字，为了严谨地计算其逆序数,我们仍需通过数学方法进行验证。

计算排列35412的逆序数

尽管从直观上看排列35412没有逆序对，但为了确保准确性并加深理解,我们可以通过以下步骤来正式计算其逆序数：

1. 定义标准排列：我们定义一个标准递增排列12345，其逆序数为0,因为不存在任何逆序对。

2. 逐一比较：我们将排列35412中的每个数字与其在标准排列12345中的对应位置进行比较,具体而言：

   • 数字3在标准排列中位于第1位之后,因此不产生逆序对；
   • 数字5在标准排列中位于第2位之后且大于其后的数字（即不与4形成逆序对）,但因位于第1位数字3之后而形成1个逆序对；
   • 数字4在标准排列中位于第3位之后且大于其后的数字（即不与5形成逆序对）,但因位于第2位数字5之前而形成1个逆序对；
   • 数字1和2在原排列中未出现,但不影响我们对已出现数字的逆序数计算。

   综上，排列35412相对于标准排列12345产生了2个逆序对（即(1, 2)和(2, 3)），但由于我们只考虑已出现数字的相对位置，实际上只计算了(2, 3)这一对，这里存在一个误解——对于完全由非连续自然数构成的排列（如本例中的35412），我们应考虑其相对于任意递增序列的“虚拟”位置变化来计算逆序数，但在此特定情况下，由于3和5均未出现在标准递增序列的前两位，它们各自仅与后续的数字形成“虚拟”逆序对（即不考虑实际未出现的前置数字），更严谨的讨论会涉及到一个更宽泛的定义或考虑“缺失”位置的虚拟影响，为简化问题并保持一致性，我们在此采用更直观的解释：即仅考虑已出现数字间的相对位置变化。

   为了学术上的严谨性，我们应指出这种解释在严格意义上并不完全符合逆序数的传统定义（即不包含未出现数字的“虚拟”影响），在更严格的数学语境下，对于非连续自然数构成的排列（如本例），通常需要额外的解释或上下文来明确其逆序数的计算方式，但在此文中，为保持简洁明了并聚焦于核心概念,我们采用上述直观解释作为示例说明。

数学公式与算法应用

虽然对于特定排列如35412的逆序数可以通过直观方法得出（在此例中为0或2基于上述讨论的简化解释），但更一般地计算任意排列的逆序数时，我们可以利用以下公式：对于长度为n的排列P，其逆序数S(P)可以表示为： [ S(P) = \sum{i=1}^{n-1} \sum{j=i+1}^{n} [P[i] > P[j]] ] [P[i] > P[j]]为布尔函数，当P[i] > P[j]时为真（计为1），否则为假（计为0），这个公式直接计算了所有可能的i和j组合中满足P[i] > P[j]的情况数量。

对于计算机科学和算法应用而言，该公式可高效地通过编程实现来计算任意给定排列的逆序数,通过双层循环遍历排列中的每对元素并检查其大小关系即可。

数学之美与实际应用

虽然排列35412的逆序数看似是一个简单的数学问题，但它背后蕴含着数学之美以及在诸多领域的应用潜力，在组合数学、统计学、计算机科学乃至物理学中,逆序数的概念都有着广泛的应用。

• 在统计学中,它可用于分析数据集的排序特性；
• 在计算机科学中,它可帮助优化算法性能评估；
• 在组合结构研究中,它揭示了不同元素间相对位置的复杂关系。

结论与展望

通过对排列35412的逆序数的探讨，我们不仅加深了对这一基础而重要数学概念的理解，还见识了其在不同领域中的广泛应用，虽然本文在解释过程中采用了简化的方法以保持问题的清晰度与可读性，但这也提醒我们在面对复杂问题时需要更加细致和严谨的态度，随着研究的深入和技术的进步，我们期待看到更多关于排列组合及其应用的新发现和新理论，而在这个充满挑战与机遇的数学世界里,每一个看似简单的例子都可能是通往更深层次理解的一把钥匙。