在数学中,排列和组合是两个基础而重要的概念，它们在解决实际问题、编程算法设计以及理论研究中都扮演着关键角色，逆序数是排列理论中的一个重要参数，它反映了排列中元素之间的相对顺序关系，本文将深入探讨排列“352416”的逆序数，并从定义、计算方法、性质及实际应用等方面进行详细阐述。

逆序数的定义

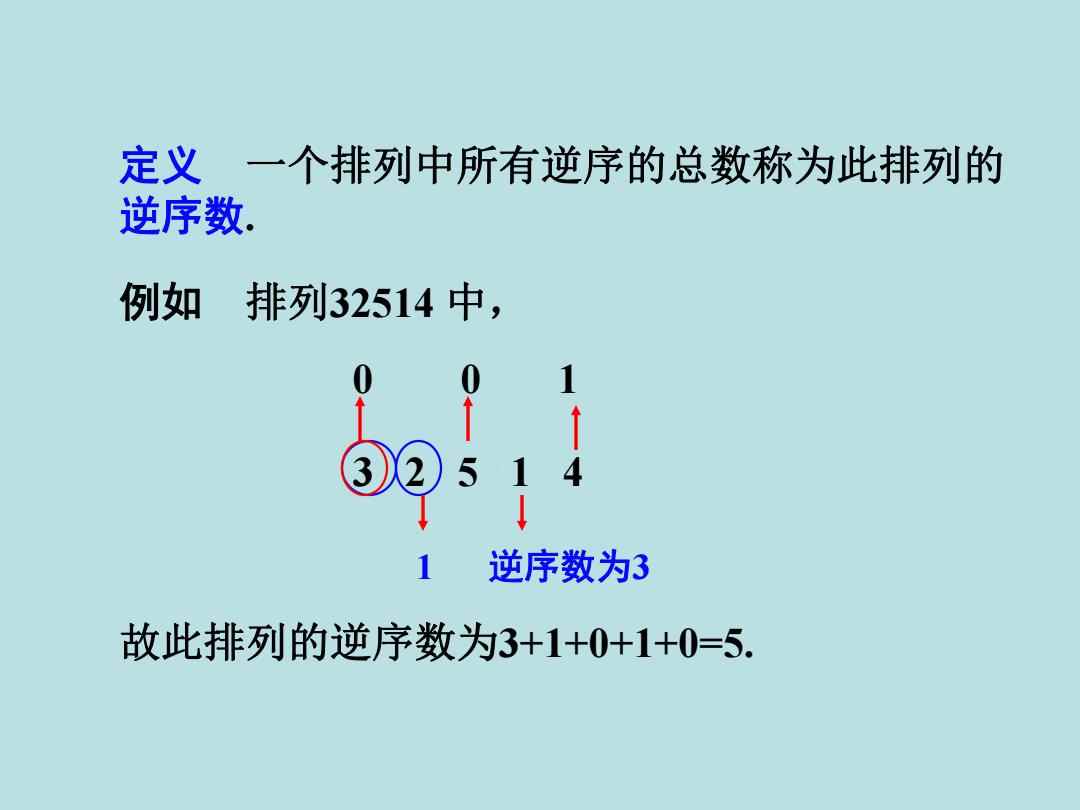
在数学中,一个排列的逆序数是指该排列中，所有不满足自然顺序（即从小到大）的元素对的数量，对于排列p1, p2, ..., pn中的任意两个元素pi和pj（i < j），如果pi > pj，则称(pi, pj)为一个逆序对，一个排列的逆序数就是其所有逆序对的数量之和。

计算排列352416的逆序数

对于排列“352416”，我们可以按照以下步骤计算其逆序数：

1. 逐一检查每个元素：从左到右遍历排列中的每个元素，对于每个元素pi，检查其右侧是否有比它小的元素。

2. 计数逆序对：每当发现一个比pi小的元素时，就增加一个逆序对计数器。

3. 应用在排列“352416”上：

   • 第一个元素“3”没有比它小的元素在右侧，所以不增加逆序对。
   • 第二个元素“5”有一个比它小的元素“4”在右侧，所以增加1个逆序对。
   • 第三个元素“2”有两个比它小的元素“4”和“1”在右侧，所以增加2个逆序对。
   • 第四个元素“4”有一个比它小的元素“1”在右侧，所以增加1个逆序对。
   • 第五个元素“1”没有比它小的元素在右侧，所以不增加逆序对。
   • 第六个元素“6”没有比它小的元素在右侧（因为它已经是最右边的了），所以不增加逆序对。

   排列“352416”的逆序数为1（来自“5”与“4”）+ 2（来自“2”与“4”和“1”）= 3个逆序对，该排列的逆序数为3。

逆序数的性质

1. 奇偶性：对于一个有n个元素的排列，其逆序数要么是奇数要么是偶数，这一性质可以通过数学归纳法证明。
2. 最大值与最小值：一个排列的逆序数最大为C(n, 2)（从n个不同元素中选取2个元素的组合数），即n(n-1)/2，而当排列为自然顺序或其反序时，其逆序数为0。
3. 与排序的关系：一个排列的逆序数与其元素的排序紧密相关，逆序数越少，说明该排列越接近自然顺序；反之，则越接近其反序。
4. 应用在算法中：在计算机科学中，如快速排序、归并排序等算法的效率分析中，逆序数是衡量数据集初始状态好坏的一个重要指标。

逆序数的计算方法

除了上述的逐一检查法外,还有以下几种计算排列逆序数的方法：

1. 直接计算法：通过遍历整个排列并计算不满足顺序的元素对数量来直接得出结果，这种方法直观但效率较低，适用于小规模数据。
2. 改进的逐一检查法：通过一些技巧减少不必要的比较来提高效率，如利用已确定的小于当前元素的右侧信息来减少后续比较次数。
3. 数学公式法：对于某些特定的排列（如1到n的自然数排列），可以通过数学公式直接计算出其逆序数，对于任意n个元素的自然顺序排列，其逆序数为n(n-1)/2，但对于非自然顺序的特定排列，如“352416”，则需逐一计算或使用其他方法。
4. 编程算法：在处理大规模数据时，可以利用编程语言中的高效算法来计算逆序数，如使用归并排序的思想进行优化等。

实际应用与意义

1. 数据预处理：在数据排序、搜索等算法中，了解数据的初始逆序数可以帮助选择更合适的算法或预处理策略，从而提高整体效率。
2. 组合数学：在组合数学中，逆序数是理解某些组合结构（如错排问题）的重要工具，通过研究不同排列的逆序数分布规律，可以解决许多复杂的组合问题。
3. 信息论与编码：在某些编码理论中，逆序数的概念被用来优化编码效率或错误检测机制，通过调整数据元素的顺序来减少编码中的逆序对数量，可以降低传输过程中的错误率或提高解码速度。
4. 机器学习与数据挖掘：在机器学习和数据挖掘领域中，数据的初始状态（包括其逆序数）可能影响算法的性能和结果，通过分析数据的统计特性（包括其逆序数），可以设计更有效的数据预处理和特征选择策略。
5. 生物信息学：在生物信息学中，基因序列的排序和比较是常见的问题之一，通过计算基因序列的逆序数，可以评估不同序列之间的相似性和差异程度，进而进行基因组比较、进化分析等研究。

结论与展望

通过对排列“352416”的逆序数的探究，我们不仅了解了如何计算一个具体排列的逆序数，还深入探讨了逆序数的定义、性质及其在多个领域中的应用和意义，逆序数是连接数学理论与实际问题的桥梁之一，它在数据分析、算法设计、组合数学等多个领域都发挥着重要作用，未来随着大数据和人工智能技术的不断发展，对逆序数及其相关问题的研究将更加深入和广泛，为解决更复杂的问题提供有力的数学工具和理论支持。