在数学与组合学领域中,排列（Permutation）与组合（Combination）是两个基础而重要的概念，排列特指从n个不同元素中取出m个元素（m≤n）进行有序排列的方式，而本文将聚焦于一个特定且有趣的排列问题——排列35，通过本文，你将深入了解排列35的原理、计算方法、应用场景以及一些有趣的数学性质，从而在理论与实践两个层面全面掌握这一概念。

排列35的基本概念

排列35,简而言之，就是从1到35这35个自然数中取出若干个不同的数进行有序排列的所有可能方式，这是一个典型的组合数学问题，其解法涉及到了阶乘（Factorial）的概念，阶乘n!表示所有小于或等于n的正整数的乘积，例如5! = 5 × 4 × 3 × 2 × 1 = 120。

排列35的直接计算法

对于排列35,最直接的计算方法是使用阶乘，由于我们需要从35个数字中取出任意数量的数字进行排列，理论上存在35的阶乘种不同的排列方式，即35! = 35 × 34 × 33 × ... × 2 × 1，由于这个数值极其庞大（远超10的60次方），直接计算或存储这样的数值在现实中是不切实际的，虽然这种方法在理论上可行，但在实际应用中我们通常采用更高效的近似或间接计算方法。

近似与间接计算法

1. 斯特林公式（Stirling's Approximation）：对于大数的阶乘计算，斯特林公式提供了一个近似但非常有效的计算方法，其公式为n! ≈ √(2πn) × (n/e)^n，其中e是自然对数的底数，虽然这个公式不能给出精确值，但它能提供一个接近真实值的估计，对于大数阶乘尤其有用，对于35!，使用斯特林公式可以快速得到一个近似的数值范围。

2. 对数与伽马函数：在更高级的数学中，可以通过对数和伽马函数（Gamma Function）来精确计算阶乘的数值，伽马函数Γ(n)可以看作是n!在实数和复数上的推广，对于整数n，有Γ(n+1) = n!，通过这种方法，我们可以得到更精确的数值结果。

   

排列35的实际应用

尽管直接计算35!在现实中不切实际，但排列的概念在多个领域有着广泛的应用：

1. 密码学与安全：在密码学中，排列常被用于生成复杂的密钥和密码组合，以增加破解难度，通过排列大量可能的数字组合，可以显著提高数据的安全性。

2. 体育赛事安排：在体育赛事中，如篮球赛、足球赛等，可以通过排列来安排不同队伍之间的比赛顺序，确保比赛的公平性和观赏性。

3. 生产与物流：在工业生产和物流管理中，排列理论可以帮助优化生产流程和货物装载顺序，提高效率和减少成本。

4. 计算机科学：在算法设计和数据分析中，排列理论被用于优化路径选择、数据排序和搜索算法等。

排列35的数学性质与特点

1. 对称性：排列具有对称性，即(a,b,c)与(b,a,c)是同一种排列的不同表示方式，这种对称性在计算时需要注意去重。

2. 周期性：对于较大的数集（如35），虽然单个排列的直接计算不现实，但可以通过数学归纳法、递归等方法研究其周期性和规律性，某些特定长度的子序列的排列规律可以用于简化问题。

3. 组合与排列的关系：虽然本文聚焦于排列35，但值得注意的是，组合（如C(n,k)）与排列紧密相关，理解它们之间的联系和区别对于深入学习组合数学至关重要，从n个元素中取k个元素进行组合的数目C(n,k)与取k个元素进行无序组合的数目C(n,k)/k!（即考虑顺序时为排列）不同。

案例分析：排列35在彩票中的应用

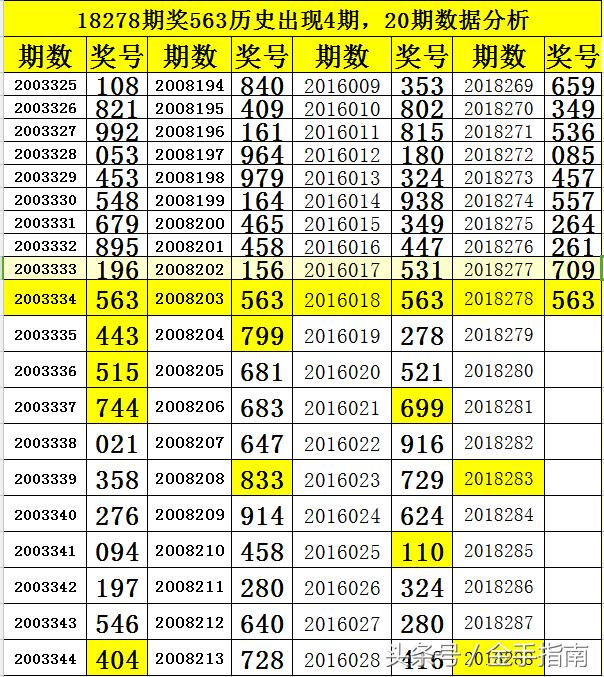
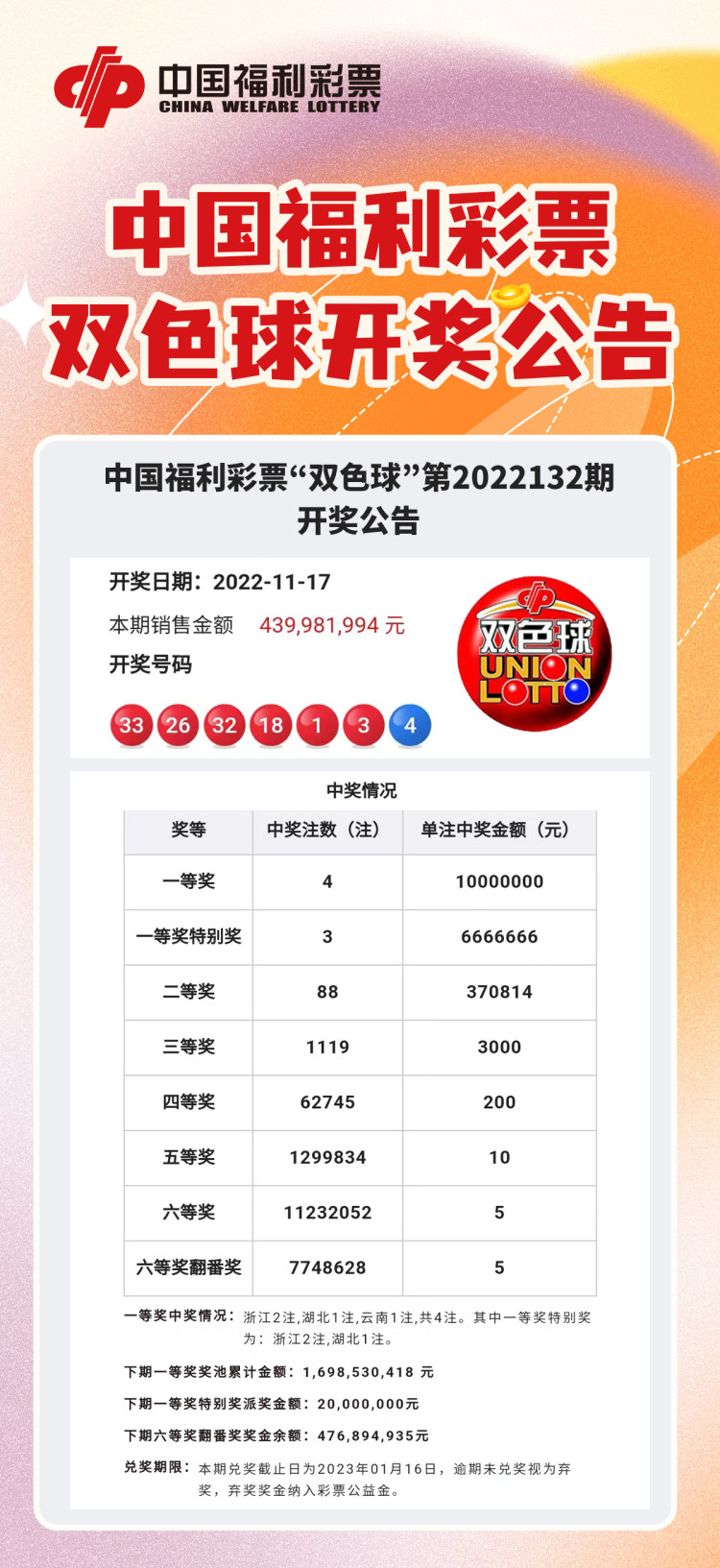
以彩票为例,许多国家的彩票游戏（如大乐透）会涉及从一定范围的数字中选取若干个数字进行组合，虽然实际开奖时并不直接计算所有可能的排列组合（因为数量过于庞大），但理解排列理论有助于设计更加公平和复杂的游戏规则，通过分析历史开奖数据中的“热号”和“冷号”，可以基于排列理论来预测未来可能的开奖号码组合，尽管这并不保证绝对的中奖率提升。

结论与展望

尽管直接计算35的所有可能排列在现实中不具可行性,但通过对排列理论的学习和理解，我们可以利用其原理和性质来解决实际问题、设计算法、优化流程等，随着计算机技术的发展和算法的优化，未来或许能开发出更高效的工具来处理这类大规模的组合问题，排列理论作为数学的一个重要分支，其深远的理论意义和应用价值将继续推动着科学、工程和技术的进步。

排列35虽然是理论上的一个挑战性概念,但它所代表的不仅仅是数学上的一个难题，更是连接理论与实践、基础与应用的桥梁，通过深入学习和理解这一概念，我们能够更好地应对现实世界中的复杂问题，为科技进步和社会发展贡献力量。